The grinding process in ball mills (where grinding balls are used as grinding medium) is one of the widely used methods in practice to reduce the size of material particles. There are quite a lot of works devoted to the detailed consideration of interaction process of the grinding balls with the particles of the material. At the same time, the number of works on the calculation of the optimal filling of the ball mill drum with grinding balls is quite small. As a rule, the optimal load is determined empirically, from theoretical studies it is possible to note the methods for calculating the best load E.V. Shelekhov, L.B. Levenson, E.A. Amosov. In the future, we will consider these methods in our publications.
As you know, grinding of material can occur due to either falling of grinding balls (waterfall mode of the mill) or due to abrasion of material particles by rolling grinding balls (cascade mode). Let’s assume that grinding of material takes place in the waterfall mode. The falling ball gains energy due to acceleration in the field of gravity, and on impact the received energy is spent on destruction of a material particle.
In order to grind the material as fast as possible, a large number of strong impacts of the grinding balls on the material are necessary. Let’s find out how the number of impacts of the ball on the material and the impact energy will depend on the filling of the drum with grinding balls.
The ball when falling moves with equal acceleration, without initial velocity, so we can write down the relationship of the path H, the time of the ball falling before impact t and the acceleration of the fall a:
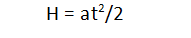
Consequently, the fall time is proportional to the square root of the traveled path, which in turn depends on the size of the ball mill drum. Obviously, the shorter the fall time, the more often the grinding bodies will hit the material loaded for grinding and, accordingly, the faster the grinding process will take place. It follows that for the fastest grinding process it is necessary that the distance covered by the falling ball should be as short as possible.
On the other hand, since the falling ball is accelerating all the time, this means that the greater the distance traveled, the more kinetic energy the milling body acquires, the stronger the impact will be, which means that the distance traveled during the fall of the ball must be as long as possible for the fastest possible milling of material.
Thus, for the fastest grinding it is necessary that the impact of the grinding body in the waterfall mode occurs as often as possible, and each impact delivers as much energy as possible to the particle of the material to be ground.
The combination of these two factors will help determine the optimum load of the ball mill drum.
As noted above, the fall time of one grinding ball is proportional to the distance traveled:
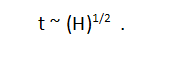
The kinetic energy E gained by the ball due to the change in potential energy is also proportional to the path H traveled:
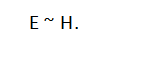
Let us introduce the notation x = (H/Hmax), and plot the dependence of the dimensionless time (t/tmax) and dimensionless energy (E/Emax) on the value x in the same coordinates.
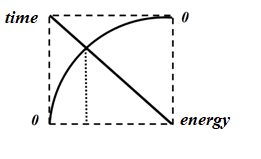
The figure shows two lines: one (curved line) represents the dependence of time (which varies from 0 to 1) on the value x, the other (straight line) represents the dependence of energy (which varies from 0 to 1) on the value x. As can be seen from the figure, these lines intersect at a certain point, and it can be expected that at this point (in other words, at a given value of the distance traveled by the grinding body) the best conditions for effective grinding of the milling material will be created.
At the point of intersection we can write:
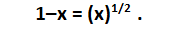
Solving this equation with respect to x, we get a number related to the proportion of the so-called “golden ratio”:

Thus, our model allows us to make the following assumption: If the ball in the mill were to fall on the material, then rise momentarily and fall again, we can expect that the best conditions for grinding would occur if the falling ball were to pass about 40 percent of the maximum possible path along a vertical line.
This leads us to the conclusion that the drum of a ball mill must be more than half filled with grinding balls.
However, it is known from experience in the use of mills that the best conditions for grinding are created when the mill is filled to about 40 percent of the volume. Consequently, our model gives a markedly overestimated value of filling of the ball mill drum.
At the same time, we understand that the grinding efficiency is influenced to a greater extent by the energy that is gained by the grinding bodies during the free fall. Indeed, the larger the free space inside the ball mill, the more kinetic energy the flying ball has time to gain before hitting the material to be ground in the waterfall mode of operation. And the rarer, stronger impacts are more effective for grinding than the more frequent, but weaker impacts.
According to L.B. Levenson, the best level of filling the drum should be about 1/3 of the vertical diameter. From this, it is easy to calculate that before hitting the material, the falling grinding body passes more than 50 … 60 percent vertically of the maximum possible path. The energy gained by the ball’s motion will, accordingly, exceed one and a half to two times the amount of energy as compared to the energy that the ball would have received after traveling 40 percent of the possible path (if air resistance is not taken into account).
Let us determine, remaining within the framework of our ideas, what will change if the mill will not work in the waterfall mode, but in the abrasion mode (cascade or mixed mode) with balls of the ground material. In this case, we will assume that the ball rolls on some inclined plane inside the drum of the ball mill.
As is known since the time of classical experiments of G. Galileo, the rolling of balls on an inclined plane is analogous to the free fall of balls under the action of gravity. Therefore, the motion of balls in this case also obeys the laws noted above (dependence of the time of motion and the acquired energy on the traversed path). Consequently, the methodology of calculation is preserved, and the calculation results will be the same as in the waterfall mode of the ball mill, that is, the number associated with the proportion of the “golden ratio” will be obtained.
Thus, in the waterfall mode of ball mill operation and in the abrasion mode, in terms of the proposed model, to achieve the best conditions for grinding the material, the falling or rolling ball must pass vertically the distance associated with the proportion of the “golden section”.
In what follows, we will look in more detail at the different methods for calculating the optimal loading of a ball mill with grinding balls. However, as practice shows, the rate of mill loading with grinding balls varies from 35 to 42%. Consequently, the method described above is quite acceptable and can be used in practice.







